Теоретическая механика - Решение задач
В категории материалов: 3236
Показано материалов: 2751-2800 |
|
В данном разделе представлены различные задачи по теоретической механике (термех) с ответами. Задачи для студентов и учащихся собраны из различных задачников и учебников, и для каждой из них есть подробное решение, а если что то неясно, можно задать вопрос в комментариях
Список учебных материалов, доступных онлайн в данной категории:
14963. 1 Груз однородный сплошной цилиндр массой 500 кг и радиусом 0,5 м лежит на движущейся платформе и удерживается от возможного перемещения по платформе упорами ступеньками. При внезапной остановке платформы цилиндр ударяется о ребро D ступеньки BD высотой 0,1 м и поднимается вверх на эту ступеньку. Далее цилиндр катится по участку DE горизонтальной площадки DK и, ударившись о другой упор наклонную плоскость KN, составляющую угол 60° с горизонтом, проходит по ней расстояние FN = 0,1 м. Качение цилиндра не сопровождается скольжением, сопротивление качению пренебрежимо мало. Отрыва цилиндра при ударах о ступеньку и о наклонную плоскость не происходит, абсолютная шероховатость ступеньки и наклонной плоскости исключает скольжение цилиндра при ударном воздействии. Определить скорость платформы до ее остановки, а также ударные импульсы, испытываемые цилиндром со стороны ступеньки и наклонной плоскости. Поверить найденные выражения угловых скоростей цилиндра после ударов о ступеньку и наклонную плоскость с помощью теоремы Карно. (решение)

14964. 13.1 Яблонский задание Д13 вариант 1. Тележка 1 общей массой 6000 кг, движущаяся со скоростью 2,5 м/с по горизонтальному прямолинейному пути, наталкивается на неподвижную тележку 2, имеющую вместе с контейнером массу 4000 кг. В конце соударения тележка 2 приобретает скорость 2 м/с, а контейнер угловую скорость вращения вокруг ребра A, закрепленного упорной планкой. Считать контейнер массой m0= 500 кг однородным прямоугольным параллелепипедом (a = 0,8 м, h = 1,5 м). Вертикальные плоскости соударения тележек полагать гладкими. Поверхность рельсов абсолютно шероховата, т. е. препятствует проскальзыванию колес при соударении тележек. Моменты инерции колес относительно их осей пренебрежимо малы. Определить скорость тележки 1 в конце соударения с тележкой 2, а также ударный импульс, воспринимаемый упорной планкой. (решение)
14965. 13.2 Яблонский задание Д13 вариант 2. Груз массой 500 кг падает с высоты 1 м в точку D абсолютно жесткой балки, имеющей шарнирно-неподвижную опору A и упругую опору B, коэффициент жесткости которой 20000 Н/см; удар груза о балку неупругий. Масса балки 6000 кг, ее длина 4 м. Горизонтальное положение балки, показанное на чертеже, соответствует статической деформации упругой опоры под воздействием веса балки. Принять балку за тонкий однородный стержень, а груз за материальную точку. Определить ударный импульс, воспринимаемый балкой в точке D, а также наибольшую деформацию упругой опоры, считая, что движение точки B происходит по прямой. (решение)
14967. 13.4 Яблонский задание Д13 вариант 4. Груз однородный сплошной цилиндр массой 200 кг и радиусом 0,2 м перемещается транспортером. Лента транспортера горизонтальна, ее постоянная скорость 0,6 м/с; скольжение ленты по шкивам 1 и 2 отсутствует. В некоторый момент времени движение транспортера внезапно прекращается. Поскольку поверхность ленты транспортера абсолютно шероховата, т. е. не допускает скольжения тела при ударном воздействии, цилиндр вследствие внезапной остановки транспортера покатится по ленте. Сопротивление качению пренебрежимо мало. Определить ударный импульс, воспринимаемый абсолютно шероховатой поверхностью ленты при внезапной остановке транспортера. Проверить найденную для этого скорость центра тяжести или угловую скорость цилиндра по теореме Карно. Определить ударный импульс, воспринимаемый упорной ступенькой высотой 0,03 м, о которую ударяется цилиндр, пройдя некоторое расстояние, если не происходят отрыв цилиндра при ударе о ступеньку и его проскальзывание. (решение)
14968. 13.5 Яблонский задание Д13 вариант 5. Транспортируемые грузы катятся из положения A без начальной скорости по наклонной плоскости, составляющей угол 15° с горизонтом, проходя вдоль нее расстояние 3 м, и продолжают катиться по горизонтальной плоскости. Скольжение отсутствует; коэффициент трения качения 0,8 см. Определить, на каком расстоянии должна быть поставлена упорная ступенька высотой 0,2 м, чтобы грузы, ударившись о ребро F ступеньки, лишь поднимались на нее, не перемещаясь дальше ребра F. Расчет произвести для груза однородного сплошного цилиндра массой 500 кг и радиусом 0,5 м. Считать, что отрыва цилиндра от ступеньки не происходит, а поверхность ступеньки абсолютно шероховата, т.е. препятствует скольжению цилиндра при ударном воздействии. Определить также горизонтальную и вертикальную составляющие ударного импульса, воспринимаемого цилиндром со стороны ступеньки, при указанных условиях. (решение)
14969. 13.6 Яблонский задание Д13 вариант 6. Маятник состоит из стержня длиной 1,2 м и однородного круглого диска радиусом 0,1 м. Масса стержня пренебрежимо мала; масса диска 5 кг. Маятник, отклоненный от положения устойчивого равновесия, падает под действием собственного веса, вращаясь вокруг неподвижной оси O; в вертикальном положении, имея угловую скорость 3 рад/с, маятник ударяется о точку B боковой грани тела D однородного прямоугольного параллелепипеда массой m = 6m0 (a = 0,8 м; b = 0,4 м; h = 0,2 м). Коэффициент восстановления при ударе 0,5. Поверхности маятника и тела D в точке соударения гладкие. Плоскость, на которой покоится тело D, абсолютно шероховата, т. е. не допускает скольжения тела при ударном воздействии. Определить угловую скорость вращения тела D вокруг ребра A в конце удара, а также ударный импульс, воспринимаемый шероховатой поверхностью в точке A (решение)
14970. 13.7 Яблонский задание Д13 вариант 7. Рычаг состоит из двух абсолютно жестких стержней AB и AD, соединенных под прямым углом. Рычаг имеет неподвижную горизонтальную ось вращения A и удерживается в точке B пружиной; AD = 1,5 м. В точку D горизонтального стержня рычага, находящегося в покое, с высоты 0,5 м падает груз массой 100 кг. Масса рычага 1000 кг, радиус его инерции относительно оси вращения 0,5 м. Положение центра тяжести рычага определяется координатами xC = 0,4 м и yC = 0,3 м. Считать груз материальной точкой, а удар груза о рычаг принять неупругим. Определить ударный импульс, испытываемый грузом, а также горизонтальную и вертикальную составляющие ударного импульса, воспринимаемого опорой A. (решение)

14971. 13.8 Яблонский задание Д13 вариант 8. На тележке 1 лежит груз однородный полый тонкостенный цилиндр массой 500 кг и радиусом 0,4 м, который удерживается от возможного перемещения по тележке ступенькой и наклонной плоскостью, составляющей угол 60° с горизонтом. Тележка 1, имеющая вместе с грузом массу 3000 кг, двигаясь по горизонтальному прямолинейному пути, наталкивается со скоростью 3 м/с на неподвижную вагонетку 2 общей массой 6000 кг. В конце соударения тележка 1 останавливается, а цилиндр, ударяясь о наклонную плоскость, начинает катиться по ней. Отрыва цилиндра при ударе о наклонную плоскость не происходит; абсолютная шероховатость наклонной плоскости исключает скольжение цилиндра при ударном воздействии. Считать вертикальные плоскости соударения тележки и вагонетки гладкими. Поверхность рельсов абсолютно шероховата, т. е. препятствует проскальзыванию колес при соударении тележек. Моменты инерции колес относительно их осей пренебрежимо малы. Определить угловую скорость цилиндра в конце удара о наклонную плоскость; проверить найденное выражение угловой скорости цилиндра по теореме Карно. Определить скорость вагонетки 2 в конце соударения с тележкой 1. (решение)
14974. 13.11 Яблонский задание Д13 вариант 11. При испытании на ударную нагрузку маятник копра массой 500 кг, отклоненный из положения устойчивого равновесия на угол 60°, падает без начальной скорости под действием собственного веса, вращаясь вокруг неподвижной оси O. В вертикальном положении маятник ударяется точкой A о середину D покоящейся вертикальной балки BF массой 2000 кг, имеющей шарнирно-неподвижную опору В и упругую опору F (BF = 2a = 3,2 м); балку можно считать однородным тонким стержнем; коэффициент восстановления при ударе 0,4. Расстояние от точки O пересечения оси вращения маятника вертикальной плоскостью его симметрии до центра тяжести C маятника OC = d = 1,5 м, а расстояние от точки O до точки A, лежащей в той же плоскости симметрии, OA = 2 м; радиус инерции маятника относительно оси вращения 1,8 м. Отклонившийся после удара на угол маятник задерживается в этом положении специальным захватом. Определить ударный импульс в точке D и расстояние от точки B от точки, в которую следует наносить удар, чтобы опора B не испытывала ударного импульса. (решение)
14975. 13.12 Яблонский задание Д13 вариант 12. Тележка 1, имеющая вместе с контейнером массу 2000 кг и движущаяся по горизонтальному прямолинейному пути со скоростью 2,5 м/с, наталкивается на тележку 2 общей массой 8000 кг, движущуюся со скоростью 0,5 м/с по тому же пути и в том же направлении. В конце соударения тележка 1 останавливается, а контейнер приобретает угловую скорость вращения вокруг ребра A, закрепленного упорной планкой. Считать контейнер массой 500 кг однородным прямоугольным параллелепипедом (a = 0,9 м, b = 1,2 м), а вертикальные плоскости соударения тележек - гладкими. Поверхность рельсов абсолютно шероховата, т. е. препятствует проскальзыванию колес при соударении тележек. Моменты инерции колес относительно их осей пренебрежимо малы. Определить угловую скорость контейнера в конце соударения тележек и проверить найденное выражение по теореме Карно. Определить скорость тележки 2 в конце соударения с тележкой 1. (решение)
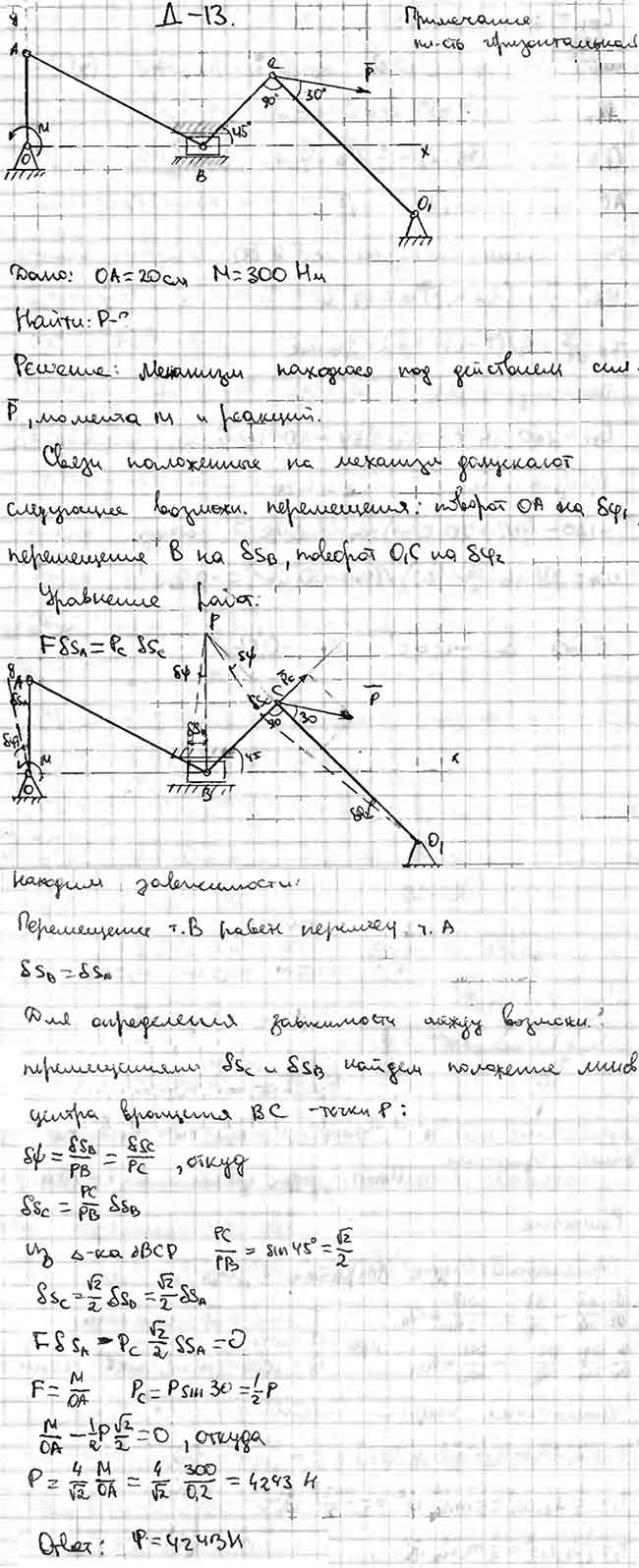
14976. 13.13 Яблонский задание Д13 вариант 13. Ось O подвеса маятника движется поступательно в горизонтальной плоскости с постоянной скоростью, при этом маятник занимает вертикальное положение относительного покоя. Радиус инерции маятника относительно оси O 0,8 м. При внезапной остановке оси подвеса маятник, находясь в том же положении и приобретя угловую скорость, ударяется точкой A о покоящееся тело D, имеющее массу 2,5m, где m масса маятника. Поверхности маятника и тела D в точке соударения гладкие. Коэффициент восстановления при соударении маятника и тела 0,6. Расстояния от точки O до точки A и до центра тяжести C маятника, отсчитываемые вдоль его вертикальной оси симметрии 1 м и 0,7 м соответственно. В конце соударения с маятником тело D приобрело скорость 0,5 м/с поступательного движения по гладкой горизонтальной плоскости. Определить- скорость оси O подвеса маятника перед внезапной остановкой, а также угол отклонения маятника после удара о тело D. (решение)
14977. 13.14 Яблонский задание Д13 вариант 14. Абсолютно жесткая конструкция, имеющая форму прямоугольного треугольника со сторонами AB =1 м и BD = 2 м, опирается на шарнирно-неподвижную опору A и удерживается в точке B пружиной. В точку D конструкции, находящейся в состоянии покоя, при котором сторона BD горизонтальна, с высоты 0,5 м падает груз массой 200 кг; удар груза неупругий. Считать конструкцию, масса которой 20000 кг, однородным треугольником, а груз материальной дочкой. Определить угловую скорость системы в конце удара и проверить найденное выражение угловой скорости по теореме Карно. Определить также ударный импульс, испытываемый опорой A. (решение)
14979. 13.16 Яблонский задание Д13 вариант 16. Вагонетка 1 общей массой 6500 кг, движущаяся по горизонтальному прямолинейному пути, наталкивается на неподвижную тележку 2, имеющую вместе с грузом массу 4000 кг. Груз однородный полый тонкостенный цилиндр массой 500 кг и радиусом 0,5 м удерживается от возможного перемещения по тележке двумя упорами ступеньками. В конце соударения вагонетка 1 и тележка 2 приобретают одинаковую скорость движения по горизонтальному прямолинейному пути, а цилиндр угловую скорость вращения вокруг ребра E ступеньки DE. Поверхность ступеньки абсолютно шероховата, т. е. препятствует проскальзыванию цилиндра при ударном воздействии; отрыва цилиндра при ударе о ребро E не происходит. После удара цилиндр поднимается на ступеньку DE высотой 0,1 м. Считать, что за время подъема цилиндра на ступеньку скорость тележки 2, приобретенная ею в конце удара, остается постоянной, а вертикальные плоскости соударения вагонетки и тележки — гладкие. Поверхность рельсов абсолютно шероховата, т. е. препятствует проскальзыванию колес при соударении тележек. Моменты инерции колес относительно их осей пренебрежимо малы. Определить ударный импульс, испытываемый цилиндром со стороны ступеньки DE, а также скорость вагонетки 1 до столкновения ее с тележкой 2. (решение)
14981. 13.18 Яблонский задание Д13 вариант 18. Абсолютно жесткая балка массой 8000 кг и длиной 4 м имеет упругую опору A и шарнирно-неподвижную опору B. Балка занимает в состоянии покоя, соответствующем статической деформации пружины A, горизонтальное положение; коэффициент жесткости пружины 10000 Н/см. Радиус инерции балки относительно горизонтальной оси вращения B 2,2 м. Балка испытывается на воздействие ударной нагрузки с помощью парового молота, в котором масса молота, штока и поршня 800 кг. Молот и связанные с ним части падают под давлением пара на середину балки с высоты 0,8 м, имея в момент соприкосновения с балкой скорость, в два раза превышающую скорость при свободном падении. Коэффициент восстановления при ударе молота о балку 0,2. Принять молот и связанные с ним элементы за материальную точку; считать, что движение точек балки происходит по прямым. Определить наибольшую деформацию упругой опоры A, считая, что молот, отскочив от балки, не падает снова, а удерживается обратным давлением пара; определить также ударный импульс, воспринимаемый опорой B. (решение)
14982. 13.19 Яблонский задание Д13 вариант 19. При испытании упорных буферных брусьев на удар маятник копра массой 500 кг, радиус инерции которого относительно неподвижной горизонтальной оси вращения O 1,2 м, отклоняют от положения устойчивого равновесия на угол 90° и отпускают без начальной угловой скорости. Падая, маятник точкой A ударяется о буферный брус массой 1000 кг, коэффициент жесткости комплекта пружин которого 10000 Н/см. Коэффициент восстановления при ударе 0,5. Отклонившийся после удара на угол маятник задерживается в этом положении специальным захватом. Расстояние от точки O пересечения оси вращения вертикальной плоскостью симметрии маятника до его центра тяжести C OC = 0,9 м; расстояние от точки O до точки A, находящейся в той же плоскости симметрии, OA =1,5 м. Пренебрегая трением скольжения бруса о горизонтальную плоскость, определить величину наибольшего сжатия буферных пружин, ударный импульс в точке A, а также расстояние от точки O до центра удара. (решение)
14984. 13.21 Яблонский задание Д13 вариант 21. Лента транспортера составляет угол 15° с горизонтом. Радиусы шкивов 0,2 м. На ленте транспортера, скольжение которой по шкивам 1 и 2 отсутствует, находится груз однородный куб массой 200 кг с ребрами длиной 0,5 м. В некоторый момент времени движение транспортера внезапно прекращается, при этом груз приобретает угловую скорость вращения вокруг ребра A, закрепленного упорной планкой. Определить наименьшую угловую скорость шкивов в момент остановки, если груз опрокидывается; определить также ударный импульс, воспринимаемый упорной планкой, при внезапной остановке шкивов, вращающихся с этой угловой скоростью. (решение)
14985. 13.22 Яблонский задание Д13 вариант 22. Груз однородный полый тонкостенный цилиндр массой 800 кг и радиусом 0,4 м покоится на движущейся платформе между упорами ступеньками. При внезапной остановке платформы ступенька AB не удерживает груз: цилиндр, поднимаясь на ступеньку, прокатывается по участку BD = 1 м горизонтальной площадки BE и ударившись о ребро F другого упора ступеньки EF высотой 0,1 м, поворачивается вокруг ребра F, вследствие чего центр тяжести цилиндра поднимается по вертикали на высоту 0,07 м. Качение цилиндра от B до F происходит без скольжения; коэффициент сопротивления качению цилиндра 0,1 см. Отрыва цилиндра при ударе о ступеньку не происходит, абсолютно шероховатая поверхность ступеньки не допускает скольжения цилиндра при ударном воздействии. Определить, какую скорость имеет центр тяжести цилиндра в начале движения на участке BD, а также ударный импульс, испытываемый ребром F ступеньки EF. (решение)
14987. 13.24 Яблонский задание Д13 вариант 24. При испытании фундамента на ударную нагрузку маятник копра, вращаясь вокруг неподвижной оси, падает из вертикального положения, показанного на чертеже, под действием собственного веса без начальной угловой скорости. В горизонтальном положении маятник точкой A ударяется о середину верхней грани покоящегося фундамента. Масса маятника 500 кг, радиус его инерции относительно оси вращения 1,8 м, масса однородного фундамента 10000 кг. Коэффициент восстановления при ударе 0,2. Отклоняющийся после удара маятник задерживается в этом положении специальным захватом. Расстояния от точки O пересечения оси вращения вертикальной плоскостью симметрии маятника до его центра тяжести C и до точки A, находящейся в той же плоскости симметрии, OC = 1,5 м и OA =2 м. Определить наибольшую упругую осадку основания, имеющего коэффициент жесткости 16 * 10&5 Н/см, ударный импульс в точке A и расстояние от точки O до центра удара. (решение)
14988. 13.25 Яблонский задание Д13 вариант 25. Тележка 1 общей массой 3000 кг, двигаясь по горизонтальному прямолинейному пути со скоростью 5 м/с, наталкивается на тележку 2, имеющую вместе с грузом массу 2000 кг и движущуюся по тому же пути и в том же направлении со скоростью 1 м/с. Груз однородный полый тонкостенный цилиндр массой 500 кг и радиусом 0,5 м удерживается от возможного перемещения по тележке двумя упорами наклонными плоскостями. В конце соударения скорости движения тележек по тому же горизонтальному прямолинейному пути изменяются, а цилиндр, ударяясь о наклонную плоскость AB, составляющую угол 60°, начинает качение по ней. Цилиндр по наклонной плоскости проходит без скольжения расстояние 0,1 м; сопротивление качению пренебрежимо мало. Отрыва цилиндра при ударе о наклонную плоскость не происходит, абсолютная шероховатость наклонной плоскости исключает скольжение цилиндра при ударном воздействии. Считать, что за время подъема цилиндра на наклонную плоскость скорость тележки 2, полученная ею в конце удара, остается постоянной, а вертикальные плоскости соударения тележек — гладкие. Поверхность рельсов абсолютно шероховата, т. е. препятствует проскальзыванию колес при соударении тележек. Моменты инерции колес относительно их осей пренебрежимо малы. Определить скорость тележки 1 в конце соударения с тележкой 2, а также ударный импульс, воспринимаемый наклонной плоскостью со стороны цилиндра (решение)
14991. 13.28 Яблонский задание Д13 вариант 28. Механизм состоит из шестерни с кулачками, которая приводится во вращение вокруг неподвижной горизонтальной оси O. Масса механизма m = 50 кг, радиус инерции относительно оси вращения i0 = 0,2 м. Механизм сбрасывает металлические болванки массой 2 кг из точки A горизонтальной плоскости AB на горизонтальную плоскость ED на расстояние 1,5 м, отсчитываемое по горизонтали от точки A. Плоскость ED расположена ниже плоскостиAB на высоту 1 м. Неупругий удар между кулачком и болванкой (k1 =0) происходит на расстоянии 0,4 м от оси вращения механизма. Коэффициент восстановления при ударе болванки о гладкую горизонтальную плоскость в точке E 0,2. Принимая болванку за материальную точку, определить угловую скорость шестерни в начале удара, а также ударные импульсы, испытываемые болванкой в точках A и E. (решение)
14992. 13.29 Яблонский задание Д13 вариант 29. Маятник, отклоненный от положения устойчивого равновесия на некоторый угол, падает без начальной скорости под действием собственного веса, вращаясь вокруг неподвижной оси O, и в вертикальном положении точкой A ударяется о покоящийся однородный полый тонкостенный цилиндр массой 200 кг и радиусом 0,2 м. Масса маятника 100 кг, радиус его инерции относительно оси вращения 1 м. Расстояния от точки O пересечения оси вращения вертикальной плоскостью симметрии до центра тяжести C маятника и до точки A, находящейся в той же плоскости симметрии, OC = 0,8 м и OA = 1,2 м. Коэффициент восстановления при соударении маятника и цилиндра 0,6. После удара цилиндр скользит, не вращаясь, по гладкой горизонтальной плоскости и, натолкнувшись на ступеньку DE высотой h = 0,05 м, поднимается на нее, не перемещаясь дальше ребра E. Отрыва цилиндра от ребра E при ударе о ступеньку не происходит, а абсолютно шероховатая поверхность ступеньки исключает проскальзывание цилиндра при ударном воздействии. Определить угол α первоначального отклонения маятника, а также ударный импульс, испытываемый цилиндром со стороны маятника. (решение)
14993. 13.30 Яблонский задание Д13 вариант 30. Рычаг состоит из двух абсолютно жестких стержней OD и OF, соединенных под прямым углом; OD = 1 м, OF = 1,5 м. Рычаг имеет шарнирно-неподвижную опору O и удерживается в точке E пружиной. Масса рычага 400 кг, радиус его инерции относительно оси вращения O 0,4 м. Рычаг находится в покос, соответствующем статической деформации пружины, при этом его стержень OD горизонтален. В точку D рычага падает груз A массой 20 кг с высоты 0,5 м. Удар груза о стержень OD рычага неупругий (k1=0). Приобретя угловую скорость, рычаг точкой F ударяется о неподвижное тело B массой 120 кг; коэффициент восстановления при этом ударе 0,2. Считать груз A и тело B материальными точками. Определить, какую скорость получает тело B в конце его соударения со стержнем OF, а также ударный импульс, воспринимаемый телом B. (решение)
|
|