Раздел: Теоретическая механика
Яблонский задание Д.21. Применение уравнений Лагранжа II рода к исследованию движения механической системы с двумя степенями свободы.
Полное условие:
Яблонский задание Д.21. Применение уравнений Лагранжа II рода к исследованию движения механической системы с двумя степенями свободы.
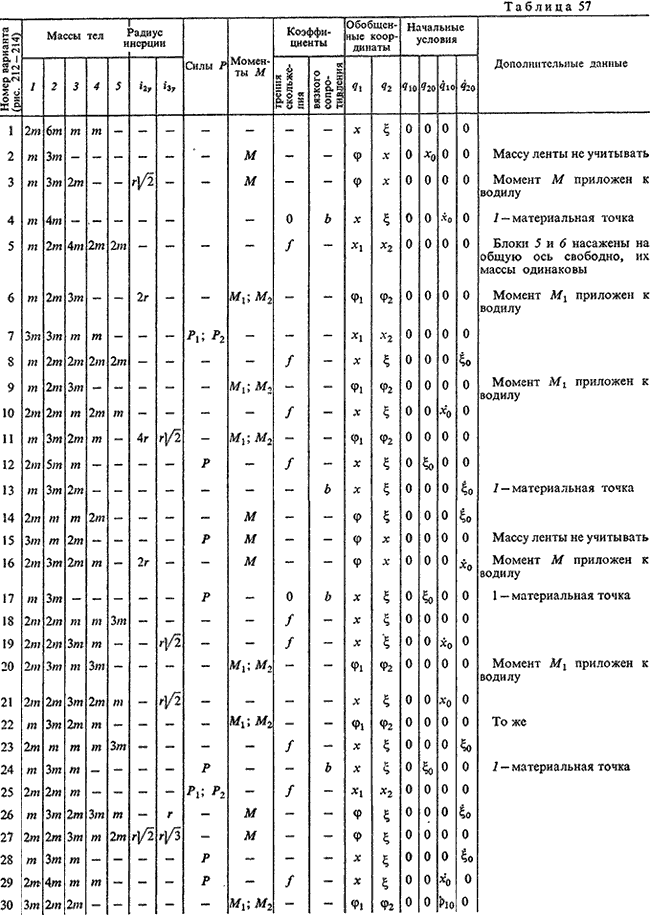
Механическая система тел 1–6 (рис. 212–214) движется под воздействием постоянных сил P и пар сил с моментами M или только сил тяжести.
Найти уравнения движения системы в обобщенных координатах q1 и q2 при заданных начальных условиях. Необходимые данные приведены в табл. 57; там же указаны рекомендуемые обобщенные координаты (x и φ – обобщенные координаты для абсолютного движения, а ξ – для относительного движения).
При решении задачи массами нитей пренебречь. Считать, что качение колес происходит без проскальзывания. Трение качения и силы сопротивления в подшипниках не учитывать. Колеса, для которых в таблице радиусы инерции не указаны, считать сплошными однородными дисками. Водила (кривошипы) рассматривать как тонкие однородные стержни. Принять, что в вариантах 6, 9, 11, 20, 22 и 30 механизм расположен в горизонтальной плоскости.
Примечания:
1. Радиус инерции тела 2 или 3 определены относительно центральной оси, перпендикулярной плоскости
чертежа.
2. Коэффициентом вязкого сопротивления назван коэффициент пропорциональности в выражении силы
сопротивления относительному движению тел 1 и 2 R=-bv, где v-относительная скорость тела.
Пример решения;
Вариант 1;
Вариант 2;
Вариант 3;
Вариант 4;
Вариант 5;
Вариант 6;
Вариант 7;
Вариант 8;
Вариант 9;
Вариант 10;
Вариант 11;
Вариант 12;
Вариант 13;
Вариант 14;
Вариант 15;
Вариант 16;
Вариант 17;
Вариант 18;
Вариант 19;
Вариант 20;
Вариант 21;
Вариант 22;
Вариант 23;
Вариант 24;
Вариант 25;
Вариант 26;
Вариант 27;
Вариант 28;
Вариант 29;
Вариант 30.
Решение, ответ задачи 15218 из ГДЗ и решебников:


