Раздел: Теоретическая механика
Яблонский задание Д.18. Применение теорем и принципов динамики к исследованию движения механической системы.
Полное условие:
Яблонский задание Д.18. Применение теорем и принципов динамики к исследованию движения механической системы.
Механическая система состоит из тела A массой mA, колеса B массой mB и электродвигателя, приводящего систему в движение. Тело A опирается на ось колеса B и на горизонтальную шероховатую плоскость. Вращающиеся части двигателя жестко связаны с колесом B, и их массы
и моменты инерции учтены соответственно в массе и моменте инерции колеса B.
Вращающий момент M(t), развиваемый электродвигателем, определяется дифференциальным уравнением
b1 dM/dt + b2M = b3 - αω, (1)
где b1, b2, b3 и α - постоянные коэффициенты, а ω - угловая скорость вращения вала двигателя. Проскальзывание колеса B по опорной плоскости отсутствует.
Корпус двигателя в вариантах 1-7, 9, 11 - 20, 30 жестко связан с телом A и его масса учтена в mA.
В вариантах 8, 10, 21—29 корпус двигателя не связан с телами A и B и, следовательно, вращающий момент является внешним по отношению к системе этих тел.
Двигатель включается в начальный момент времени (t = 0), когда система находится в покое. Наличие силы трения покоя (сцепления), приложенной к телу A со стороны опорной плоскости, приводит к тому, что движение механической системы начинается только через т с после включения двигателя. Затем скорость поступательного движения системы возрастает до некоторого значения v*. В дальнейшем производится торможение и скорость поступательного движения системы на пути s снижается до значения 0,9v*.
Требуется:
1. Определить зависимость M = M (t) при 0 ≤ t ≤ т, значение Mн = M (t) в начальный момент движения и время т.
2. Определить зависимость v = v (t) при t ≥ т, найти значение установившейся скорости v*, и значение установившегося момента М*.
3. На этапе торможения определить пути, проходимые системой при снижении v до значения 0,9v*, для двух режимов торможения.
1-й режим - торможение двигателем - двигатель работает как тормоз.
При этом момент на валу двигателя определяется уравнением
b1 dM/dt = -αω.
2-й режим — механическое торможение. При этом M = const = 0.
Сравнить пути торможения s и l при первом и втором режимах торможения.
Схемы механизмов приведены на рис. 193-195, а необходимые данные для расчета - в таблице 54.
На рис. 193 - 195 С - центр тяжести тела A, O - центр тяжести однородного колеса B, стрелкой указано направление движения; D — точка опирания тела A на шероховатую поверхность.
В вариантах 9,11, 30 при разгоне тело A контактирует с опорной поверхностью в точке D, а при торможении - в точке D1.
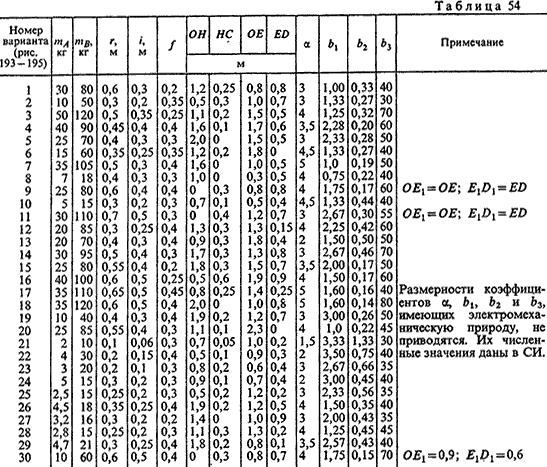
В табл. 54 приведены значения следующих параметров:mA, mB - массы тел A и B; r - радиус колеса B; i - радиус инерции колеса B относительно оси вращения; f - коэффициент трения, OH, HC, OE, ED - см. рис. 193 - 195, α, b1, b2, b3 - постоянные коэффициенты.
Примечание. Размерности коэффициентов α, b1, b2 и b3 имеющих электромеханическую природу, не приводятся. Их численные значения даны в СИ.
Пример решения;
Вариант 1;
Вариант 2;
Вариант 3;
Вариант 4;
Вариант 5;
Вариант 6;
Вариант 7;
Вариант 8;
Вариант 9;
Вариант 10;
Вариант 11;
Вариант 12;
Вариант 13;
Вариант 14;
Вариант 15;
Вариант 16;
Вариант 17;
Вариант 18;
Вариант 19;
Вариант 20;
Вариант 21;
Вариант 22;
Вариант 23;
Вариант 24;
Вариант 25;
Вариант 26;
Вариант 27;
Вариант 28;
Вариант 29;
Вариант 30.
Решение, ответ задачи 15122 из ГДЗ и решебников:


